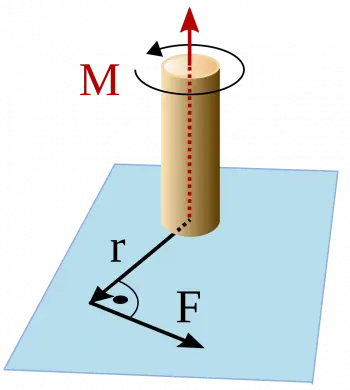
Das Moment einer Kraft, auch „Drehmoment“ genannt, ist eine physikalische Größe, die die Tendenz einer Kraft misst, ein Objekt um einen Punkt oder eine Drehachse zu drehen.
Das Moment einer Kraft hängt mit den Newtonschen Gesetzen zusammen, da die Größe der ausgeübten Kraft die Winkelbeschleunigung des Objekts beeinflusst (zweites Gesetz) und weil das durch die Kraft auf ein Objekt erzeugte Moment auch eine gleiche, aber entgegengesetzte Kraft auf das Objekt erzeugt. Richtung der Rotationsachse oder auf ein anderes Objekt (drittes Gesetz).
Mathematisch ist das Moment einer Kraft definiert als das Produkt aus dem Wert der Kraft (F) und dem senkrechten Abstand (r) vom Angriffspunkt der Kraft zur Rotationsachse.
Das Moment einer Kraft kann in verschiedenen Situationen berechnet werden, entweder im Kontext eines ruhenden Objekts (statisch) oder in Bewegung (dynamisch).
Formel für das Moment einer Kraft
Die Formel zur Berechnung des Moments (τ) einer Kraft (F) in Bezug auf einen Punkt oder eine Drehachse unter Berücksichtigung des senkrechten Abstands (r) vom Angriffspunkt der Kraft zur Drehachse lautet wie folgt folgt:
Moment (τ) = F × r
Wo:
-
τ = Kraftmoment (Drehmoment) in der Einheit Newtonmeter (Nm) oder Fuß-Pfund (lb-ft)
-
F = Größe der ausgeübten Kraft, gemessen in Newton (N) oder Pfund (lb)
-
r = Senkrechter Abstand vom Angriffspunkt der Kraft zur Drehachse, gemessen in Metern (m) oder Fuß (ft)
Diese Formel gilt, wenn Kraft und Abstand senkrecht zueinander stehen, das heißt, die Kraft wirkt in eine Richtung, die einen Winkel von 90 Grad zum Radius bzw. Abstand zur Drehachse bildet.
In Situationen, in denen Kraft und Abstand nicht senkrecht zueinander stehen, müssen Konzepte von Vektoren oder Trigonometrie verwendet werden, um die Kraft in ihre Komponenten senkrecht zum Radius aufzulösen, wodurch das resultierende Moment berechnet werden kann.
Bei Vektoren folgt die Richtung des Impulses je nach Konvention entweder der Rechte-Hand-Regel oder der Korkenzieherregel. Das bedeutet, dass das Moment je nach Wirkungsrichtung der Kraft relativ zur Drehachse positiv oder negativ sein kann.
Beispiele
Das Moment einer Kraft findet in unserem täglichen Leben in verschiedenen Situationen häufig Anwendung. Hier sind einige Beispiele dafür, wie das Moment einer Kraft im Alltag angewendet wird:
-
Öffnen von Türen: Wenn Sie einen Türgriff drehen, um ihn zu öffnen, üben Sie einen Moment auf die Scharniere aus. Je weiter die aufgebrachte Kraft von den Scharnieren entfernt ist, desto einfacher lässt sich die Tür öffnen, da das Moment zunimmt und weniger Kraft zum Drehen erforderlich ist.
-
Schrauben festziehen: Wenn Sie eine Schraube mit einem Schraubenschlüssel festziehen, üben Sie ein Moment um die Achse der Schraube aus. Die Länge des Schraubenschlüssels (Abstand von der Schraubenachse) beeinflusst die Kraft, die Sie aufwenden müssen, um die Schraube erfolgreich festzuziehen.
-
Drehen eines Schraubenschlüssels: Wenn Sie Muttern und Schrauben mit einem Schraubenschlüssel lösen oder festziehen, üben Sie ein Moment um die Achse der Schraube aus. Auch hier bestimmt die Länge des Schraubenschlüssels die Menge des erzeugten Moments und damit die Leichtigkeit, mit der sich die Mutter oder Schraube drehen lässt.
-
Autolenkrad: Wenn Sie das Lenkrad eines Autos drehen, um die Richtung zu ändern, üben Sie einen Moment um die Lenkachse des Fahrzeugs aus. Je weiter Sie das Lenkrad von der Lenkachse drehen, desto schneller ändert sich die Richtung des Fahrzeugs.
-
Schwingen auf einer Schaukel: Beim Schwingen üben Sie Schwung auf die Haken der Schaukel aus. Indem Sie Ihre Füße beim Sitzen auf der Schaukel hin und her bewegen, kontrollieren Sie den Schwung und bestimmen die Reichweite und Geschwindigkeit der Bewegung.
-
Fahrrad: Wenn auf die Pedale eines Fahrrads eine Kraft ausgeübt wird, entsteht ein Kraftmoment in Bezug auf die Pedalachse. Ebenso hängt die Kraft, die auf die Kette übertragen wird, direkt vom Radius der Kettenblätter ab, also dem Abstand vom Rotationszentrum.
-
Hebel: Ein Hebel ist eine einfache Maschine, die aus einer starren Stange besteht, die um einen festen Punkt, den sogenannten Drehpunkt, schwenkt. Durch das Aufbringen einer Kraft auf ein Ende des Hebels (Eingangskraft) wird ein Moment erzeugt, das das Anheben einer Last am anderen Ende ermöglicht (Ausgangskraft).
-
Riemenscheibe: Eine Riemenscheibe ist ein Rad, durch das ein Seil oder Kabel läuft. Durch Ziehen an einem Ende des Seils (Eingangskraft) wird ein Moment auf die Rolle ausgeübt, wodurch eine Last am anderen Ende angehoben werden kann (Ausgangskraft).
-
Dampfturbine: Die in den elektrischen Generatoren eines Kernkraftwerks verwendeten Dampfturbinen sind so konstruiert, dass der Dampf eine tangentiale Kraft zum Rad und senkrecht zur Achse erzeugt, sodass ein Kraftmoment erzeugt wird, um eine Kreisbewegung zu erreichen .
Gelöste Übungen
Aufgabe 1: Moment einer Kraft senkrecht zur Drehachse
Angenommen, wir haben eine Tür, die sich um ihre Scharniere dreht, und wir üben eine Kraft von 20 Newton in der Richtung senkrecht zur Drehachse in einem Abstand von 0,5 Metern von der Drehachse zum Angriffspunkt der Kraft aus. Berechnen Sie das Kraftmoment.
Lösung
Das Kraftmoment würde wie folgt berechnet:
Moment (τ) = F × r
τ = 20 N × 0,5 m
τ = 10 Nm
Das auf die Tür wirkende Kraftmoment beträgt 10 Newtonmeter (Nm).
Aufgabe 2: Moment einer Kraft, die nicht senkrecht zur Drehachse steht
Nehmen wir nun an, wir üben eine Kraft von 30 Newton auf dieselbe Tür aus, aber dieses Mal wirkt die Kraft in einem Winkel von 60 Grad zur Drehachse, und der Abstand von der Drehachse zum Angriffspunkt der Kraft beträgt 1 Meter. Berechnen Sie das Kraftmoment.
Lösung
Um das Moment zu berechnen, müssen wir zunächst die Kraft in ihre Komponenten senkrecht zum Radius auflösen.
Kraft senkrecht zum Radius (Fsenkrecht ) = F × cos(θ)
Fsenkrecht = 30 N × cos(60°)
Fsenkrecht = 30 N × 0,5
Fsenkrecht = 15 N
Moment (τ) = Fsenkrecht × r
τ = 15 N × 1 m
τ = 15 Nm
Das auf die Tür wirkende Kraftmoment beträgt unter Berücksichtigung seiner Komponente senkrecht zum Radius 15 Newtonmeter (Nm).