
Die Zentripetalkraft ist ein physikalisches Konzept, das in der Kinematik und insbesondere in der Kreisbewegung eine entscheidende Rolle spielt.
Trotz ihrer Bedeutung für das Verständnis alltäglicher und natürlicher Phänomene wird sie oft missverstanden oder mit der Zentrifugalkraft verwechselt.
In diesem Artikel erklären wir anhand einiger Beispiele aus dem Alltag, was Zentripetalkraft ist, damit Sie ihre Bedeutung besser verstehen.
Definition: Was ist Zentripetalkraft?
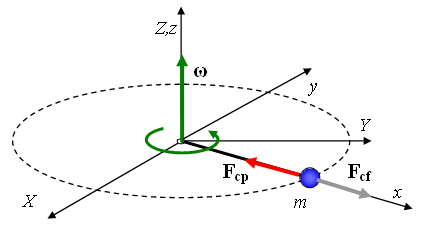 Die Zentripetalkraft ist eine Kraft, die auf ein Objekt wirkt, das sich auf einer Kreisbahn bewegt. Seine Richtung zeigt immer auf den Mittelpunkt des Kreises, in dem sich das Objekt bewegt. Diese Kraft ist notwendig, damit sich das Objekt auf einer Kreisbahn statt auf einer geraden Linie bewegt.
Die Zentripetalkraft ist eine Kraft, die auf ein Objekt wirkt, das sich auf einer Kreisbahn bewegt. Seine Richtung zeigt immer auf den Mittelpunkt des Kreises, in dem sich das Objekt bewegt. Diese Kraft ist notwendig, damit sich das Objekt auf einer Kreisbahn statt auf einer geraden Linie bewegt.
Es wird oft mit der Definition von „Zentrifugalkraft“ verwechselt, aber es ist wichtig zu verstehen, dass Zentrifugalkraft eher eine scheinbare Illusion ist, die durch die Trägheit von Objekten in Kreisbewegung verursacht wird.
6 Beispiele für Zentripetalkraft
Die Zentripetalkraft ist ein grundlegender Bestandteil vieler Aspekte des Alltagslebens und der modernen Technologie.
Hier sind einige bemerkenswerte Beispiele:
1. Fahrzeuge in Kurven
Wenn ein Auto durch eine Kurve fährt, erfährt es eine Zentripetalkraft, die es in der Spur hält. Die benötigte Zentripetalkraft hängt von der Geschwindigkeit des Autos, dem Kurvenradius und der Masse des Fahrzeugs ab.
Wenn ein Zug eine Kurve fährt, üben die Schienen eine Seitenkraft auf die Spurkränze der Wagenräder aus und zwingen ihn so, seine Bahn zu ändern.
2. Achterbahnen
Ein weiteres gutes Beispiel sind Achterbahnen: Wenn ein Achterbahnauto durch Loopings und Kurven fährt, erfährt es Zentripetalkräfte, die es entlang der Strecke in Bewegung halten.
Der Spaß und die Spannung einer Achterbahn sind zum Teil auf diese kontrollierten Zentripetalkräfte zurückzuführen.
3. Radfahren und Motorradfahren
 Radfahrer und Motorradfahrer verlassen sich auf die Zentripetalkraft, um bei Kurvenfahrten in Position zu bleiben. Durch die Neigung zur Innenseite der Kurve kann die Zentripetalkraft die Trägheit des Fahrers ausgleichen und ihn auf dem Weg halten, ohne zu stürzen.
Radfahrer und Motorradfahrer verlassen sich auf die Zentripetalkraft, um bei Kurvenfahrten in Position zu bleiben. Durch die Neigung zur Innenseite der Kurve kann die Zentripetalkraft die Trägheit des Fahrers ausgleichen und ihn auf dem Weg halten, ohne zu stürzen.
4. Zentrifugen
Zentrifugen sind Geräte, die in Laboren und in der Industrie eingesetzt werden, um Bestandteile einer Mischung anhand ihrer Dichte zu trennen.
Auf die rotierende Probe wird eine Zentripetalkraft ausgeübt, die dazu führt, dass sich die schwereren Partikel nach unten und die leichteren Partikel nach oben bewegen, wodurch eine Trennung ermöglicht wird.
5. Satelliten und Raumfahrzeuge
Satelliten und Raumfahrzeuge im Orbit um die Erde oder andere Himmelskörper sind Beispiele, die auf der Zentripetalkraft beruhen, um auf ihrer Umlaufbahn zu bleiben. Diese Kraft wirkt der Anziehungskraft der Schwerkraft entgegen und ermöglicht es Weltraumobjekten, in konstanter Orbitalbewegung zu bleiben. Sie ist ein wichtiger Bestandteil beim Studium der Astronomie.
6. Windkraftanlagen
Windenergie ist eine Energieart, die Windenergie in Strom umwandelt. Diese Funktion übernehmen Windkraftanlagen, deren Rotorblätter unter Berücksichtigung der Zentripetalkraft ausgelegt sein müssen, der sie bei voller Rotation standhalten müssen.
7. Zyklone und Tornados
Zyklone und Tornados sind rotierende Wettersysteme, die sich aufgrund der Zentripetalkraft bilden. Die Rotation der Erde und andere meteorologische Faktoren sorgen für diese beeindruckenden Naturphänomene.
Zentripetalkraftformel
Die Zentripetalkraft wird nach folgender Gleichung berechnet:
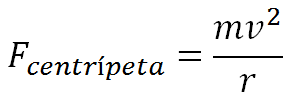
Wo:
-
Fc ist die Zentripetalkraft.
-
m ist die Masse des bewegten Objekts.
-
v ist die Tangentialgeschwindigkeit des Objekts.
-
r ist der Radius der Kreisbahn.
Diese Gleichung zeigt, dass die Zentripetalkraft direkt proportional zur Masse des Objekts und dem Quadrat seiner Tangentialgeschwindigkeit ist. Darüber hinaus ist die Zentripetalkraft umgekehrt proportional zum Radius der Kreisbahn.
Mit anderen Worten: Bei einer höheren Tangentialgeschwindigkeit oder einem kleineren Radius ist eine größere Zentripetalkraft erforderlich, um das Objekt auf seiner Kreisbahn zu halten.
Der Ursprung der Zentripetalkraft
Die Zentripetalkraft hat ihre Wurzeln in den Grundgesetzen der Physik, insbesondere im zweiten Newtonschen Gesetz. Nach diesem Gesetz ist die Beschleunigung eines Objekts direkt proportional zur ausgeübten Kraft und umgekehrt proportional zu seiner Masse.
Im Zusammenhang mit einer Kreisbewegung bedeutet dies, dass eine Nettokraft zum Kreismittelpunkt hin erforderlich ist, um den geradlinigen Weg zu verändern.
Um dieses Konzept besser zu verstehen, betrachten wir das klassische Beispiel eines Spinnseils, an dessen Ende eine Masse befestigt ist. Wenn sich das Objekt am Ende der Schnur dreht, erfährt es eine Zentripetalkraft, die es auf seiner Umlaufbahn hält.
Diese Kraft entsteht durch die Spannung in der Saite und wirkt als Nettokraft, die auf die Mitte des Rotationskreises gerichtet ist.
Anwendung in der Nuklearindustrie
 In der Nuklearindustrie werden derartige Kräfte auch zur Erzielung von Kernfusionsreaktionen eingesetzt. In einem Kernfusionsreaktor spielt die Zentripetalkraft eine wesentliche Rolle, bei Reaktoren, die auf Trägheits- oder magnetischem Einschluss basieren.
In der Nuklearindustrie werden derartige Kräfte auch zur Erzielung von Kernfusionsreaktionen eingesetzt. In einem Kernfusionsreaktor spielt die Zentripetalkraft eine wesentliche Rolle, bei Reaktoren, die auf Trägheits- oder magnetischem Einschluss basieren.
Im speziellen Fall von Reaktoren mit magnetischem Einschluss wie dem Tokamak erzeugen Magnetfelder Zentripetalkräfte, die dazu beitragen, das geladene Plasma (eine Mischung aus Ionen und Elektronen bei hohen Temperaturen) auf kreisförmigen oder spiralförmigen Bahnen im Reaktor einzuschließen.
Ziel ist es, zu verhindern, dass das Plasma die Wände des Reaktors berührt, da dieser dadurch gekühlt und eine Fusion verhindert werden könnte. Diese Zentripetalkräfte werden erzeugt, um der Tendenz des Plasmas entgegenzuwirken, sich aufgrund der enormen Drücke und Temperaturen, die darin erzeugt werden, auszudehnen.