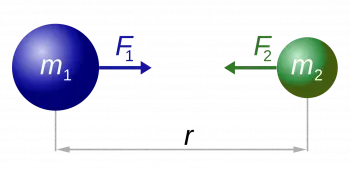
Newtons Gesetz der universellen Gravitation ist einer der Grundpfeiler der Physik und wurde im 17. Jahrhundert von Sir Isaac Newton entwickelt. Dieses Gesetz beschreibt die Anziehungskraft zwischen zwei Körpern aufgrund ihrer Masse und relativen Entfernung.
Es ist eines der wichtigsten und am weitesten verbreiteten Gesetze im Bereich der klassischen Physik und hat es ermöglicht, viele Phänomene im Universum zu verstehen und vorherzusagen.
In diesem Artikel werden wir im Detail untersuchen, was das Gesetz der universellen Gravitation ist, seine Formel, seine Bedeutung und einige Beispiele, die seine Anwendung veranschaulichen.
Was ist das Gesetz der universellen Gravitation?
Das Gesetz der universellen Gravitation besagt, dass die Anziehungskraft zwischen zwei Körpern direkt proportional zum Produkt ihrer Massen und umgekehrt proportional zum Quadrat des Abstands zwischen ihnen ist.
Das heißt, je größer die Masse der Objekte und je näher sie beieinander sind, desto größer ist die Anziehungskraft zwischen ihnen.
Die Formel des Gesetzes der universellen Gravitation:
Die mathematische Formel zur Berechnung der Gravitationskraft zwischen zwei Objekten lautet wie folgt:
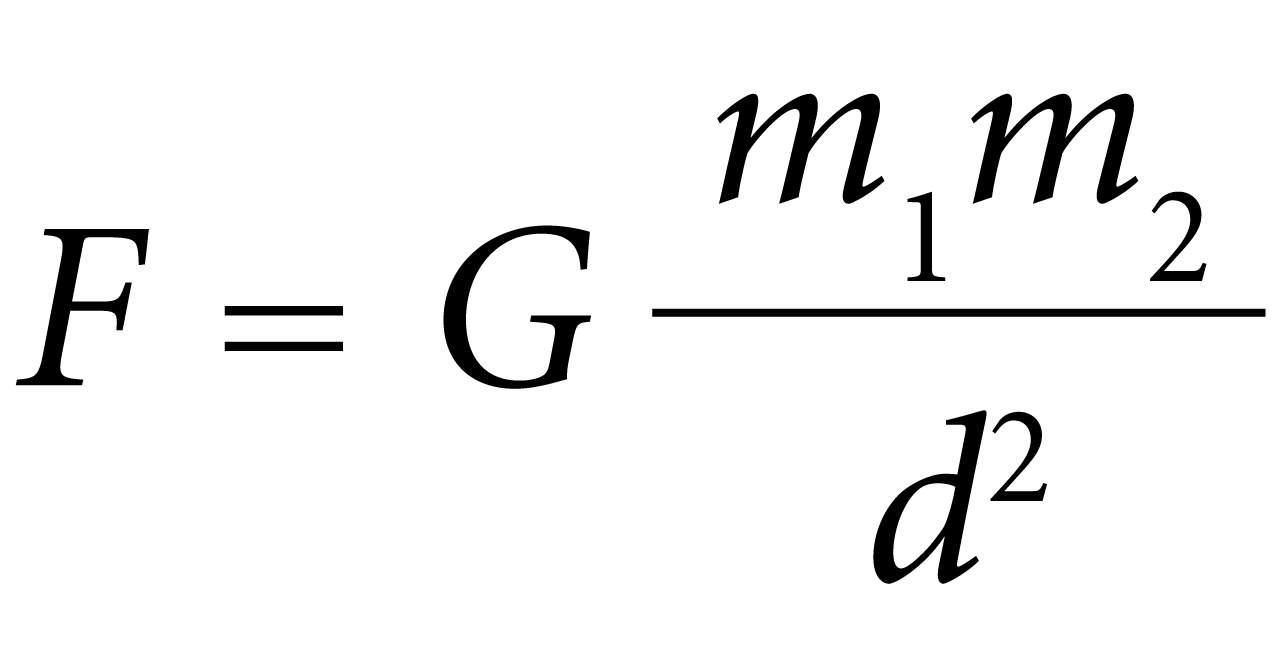
Wo:
-
F ist die Gravitationskraft zwischen Objekten, ausgedrückt in Newton,
-
G ist die universelle Gravitationskonstante, ungefähr 6,674 × 10 -11 N (m/kg) 2
-
m 1 und m 2 sind die Massen der Objekte, ausgedrückt in Kilogramm (kg).
-
r ist der Abstand zwischen den Massenschwerpunkten von Objekten, ausgedrückt in Metern (m).
Die universelle Gravitationskonstante (G) hat einen Wert von etwa 6,674 × 10 -11 N (m/kg) 2 und wird verwendet, um die Anziehungskraft als Funktion der verwendeten Massen- und Entfernungseinheiten zu skalieren.
Bedeutung des Gesetzes der universellen Gravitation:
Das Gesetz der universellen Gravitation ist für die Erforschung und das Verständnis des Universums von größter Bedeutung. Mithilfe dieses Gesetzes können wir Phänomene wie die Umlaufbahn der Planeten um die Sonne, die Bewegungen der Monde um die Planeten und die Wechselwirkung zwischen massiven Objekten im Weltraum erklären und vorhersagen.
Darüber hinaus hat das Recht auch praktische Anwendungen im Alltag. Es ermöglicht beispielsweise das Verständnis der Funktionsweise künstlicher Satelliten, die die Erde umkreisen, und ist für die Weltraumnavigation und die Planung von Weltraummissionen von entscheidender Bedeutung.
Beispiele für die Anwendung des Gesetzes der universellen Gravitation:
Nachfolgend zeigen wir 4 Beispiele, in denen das Newtonsche Gesetz der universellen Gravitation angewendet wird:
1. Die Umlaufbahn der Erde um die Sonne
Die Gravitationskraft zwischen Erde und Sonne ist dafür verantwortlich, dass sich unser Planet in einer stabilen Umlaufbahn um den Stern befindet.
Diese Kraft ermöglicht es der Erde, sich kreisförmig um die Sonne zu bewegen und bestimmt den Zeitraum eines Jahres. Die Kraft, die die Sonne auf die Erde ausübt, steht in jedem Moment senkrecht zur linearen Geschwindigkeit der Erde.
2. Der Mond und die Gezeiten
Für die Gezeiten ist die Gravitationskraft zwischen Erde und Mond verantwortlich. Der Mond übt eine Anziehungskraft auf die Ozeane aus, wodurch der Wasserspiegel steigt und fällt, wenn sich die Erde dreht.
Wie die Sonne und die Erde ist diese Kraft die Zentripetalkraft, die den Mond dazu zwingt, die Erde zu umkreisen.
3. Künstliche Satelliten
Bei der Konstruktion und dem Betrieb künstlicher Satelliten wird auch mit der Formel des Gesetzes der universellen Gravitation gerechnet.
Um einen Satelliten im Orbit zu halten, ist eine bestimmte Geschwindigkeit und Höhe erforderlich, um die Gravitationskraft mit der durch die Orbitalbewegung erzeugten Zentrifugalkraft auszugleichen.
4. Herabfallende Gegenstände
Das Gesetz gilt auch für herabfallende Gegenstände auf der Erdoberfläche. Je größer die Masse des Objekts ist, desto größer ist die auf es wirkende Gravitationskraft und desto schneller fällt es.
Übungen zum Gesetz der universellen Gravitation
Nachfolgend zeigen wir drei gelöste Aufgaben, die die Anwendung dieses physikalischen Gesetzes veranschaulichen:
Übung 1: Berechnung der Gravitationskraft zwischen zwei Körpern
Angenommen, wir haben zwei Objekte: eines mit einer Masse von 5 kg und das andere mit einer Masse von 8 kg. Der Abstand zwischen den Massenschwerpunkten der Objekte beträgt 2 Meter. Wir wollen die Gravitationskraft zwischen ihnen berechnen.
Daten
-
m1 = 5kg
-
m2 = 8kg
-
r=2m
-
G = 6,674 × 10 -11 N (m/kg) 2
Lösung:
Wir verwenden die Formel des Gesetzes der universellen Gravitation:
F = G (m 1 m 2 ) / r 2
Ersetzen der bekannten Werte:
F = (6,674 × 10 -11 N (m/kg) 2 ) * (5 kg * 8 kg) / (2 m) 2
F = 6,674 × 10 -10 N
Daher beträgt die Gravitationskraft zwischen den beiden Körpern etwa 6,674 × 10 -10 N.
Übung 2: Berechnung der Gravitationskraft zwischen der Erde und einem Objekt
Angenommen, wir möchten die Gravitationskraft zwischen der Erde (Masse ≈ 5.972 × 1024 kg) und einem Objekt mit einer Masse von 100 kg berechnen. Der Abstand zwischen dem Erdmittelpunkt und dem Objekt beträgt 6,371 × 10^6 Meter (ungefährer Erdradius).
Daten:
-
m 1 (Masse der Erde) = 5,972 × 10 24 kg
-
m 2 (Masse des Objekts) = 100 kg
-
r (Entfernung) = 6,371 × 10 6 m
-
G = 6,674 × 10 -11 N (m/kg) 2
Lösung:
Wir wenden die Formel des Gesetzes der universellen Gravitation an:
F = G (m 1 m 2 ) / r 2
Ersetzen der bekannten Werte:
F = (6.674 × 10-11 N (m/kg) 2 ) * ((5.972 × 1024 kg) * (100 kg)) / (6.371 × 106 m)2
F = 981,95 N
Daher beträgt die Gravitationskraft zwischen der Erde und dem Objekt etwa 981,95 N.
Aufgabe 3: Berechnung der Masse eines Objekts aus der Gravitationskraft
Angenommen, wir haben zwei Objekte und wissen, dass die Gravitationskraft zwischen ihnen 100 N beträgt. Der Abstand zwischen den Objekten beträgt 10 Meter und die Masse eines der Objekte beträgt 5 kg. Wir wollen die Masse des zweiten Objekts berechnen.
Daten:
-
F = 100N
-
r = 10m
-
m1 = 5kg
-
G = 6,674 × 10 -11 N (m/kg) 2
Lösung:
Wir verwenden die Formel des Gesetzes der universellen Gravitation und löschen m2:
F = G (m 1 m 2 ) / r 2
Wir räumen m2:
m 2 = (F * r 2 ) / (G * m 1 )
Ersetzen der bekannten Werte:
m 2 = (100 N * (10 m) 2 ) / ((6,674 × 10 -11 N (m/kg) 2 ) * 5 kg)
m 2 ≈ 2,997 × 10 13 kg
Daher beträgt die Masse des zweiten Objekts ungefähr 2,997 × 10 13 kg.