Eine gleichmäßig beschleunigte Kreisbewegung (UACM) ist eine Bewegungsart, bei der sich ein Objekt mit konstanter Beschleunigung auf einer Kreisbahn bewegt.
Der MCUA ist eine Bewegungsart, die für die Berechnung der Kinematik eines Körpers von entscheidender Bedeutung ist. Dieses Phänomen ist für das Verständnis einer Vielzahl von Situationen von grundlegender Bedeutung, von der Fahrzeugmechanik bis zur Dynamik umlaufender Planeten, und kann durch spezifische Formeln beschrieben werden, die Winkelgeschwindigkeit, Winkelbeschleunigung und Zeit in Beziehung setzen.
Was ist eine gleichmäßig beschleunigte Kreisbewegung?
Die gleichmäßig beschleunigte Kreisbewegung (UACM) ist ein grundlegendes Konzept der Physik, das die Bewegung eines Objekts entlang einer Kreisbahn mit konstanter Beschleunigung beschreibt.
Im Gegensatz zu einer geradlinigen Bewegung, bei der sich ein Objekt geradlinig bewegt, beinhaltet MCUA eine konstante Änderung der Winkelgeschwindigkeit des Objekts, wodurch es sich entlang einer geschlossenen Kurve dreht.
Im MCUA ist die Winkelbeschleunigung des Objekts konstant, was bedeutet, dass seine Winkelgeschwindigkeit mit der Zeit gleichmäßig zunimmt oder abnimmt.
Grundlegende Merkmale der Bewegung
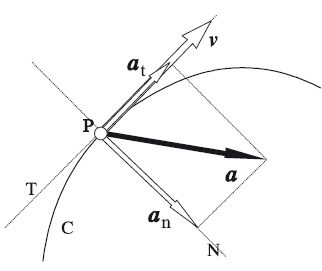Die grundlegenden Merkmale, die diese Bewegung definieren, sind:
- Das Objekt bewegt sich auf einer Kreisbahn. Dies impliziert das Auftreten einer Zentripetalbeschleunigung, um den Abstand des Objekts vom Rotationszentrum konstant zu halten.
- Die Winkelgeschwindigkeit erfährt eine konstante Winkelbeschleunigung, daher erfährt auch die Tangentialgeschwindigkeit eine Tangentialbeschleunigung.
Grundlegendes Konzept
Winkelgeschwindigkeit
Die Winkelgeschwindigkeit, dargestellt durch den griechischen Buchstaben „ω“ (Omega), ist ein Maß dafür, wie schnell sich ein Objekt entlang einer Kreisbahn dreht. Sie wird im Bogenmaß pro Sekunde (rad/s) gemessen.
Tangentialgeschwindigkeit
Die Tangentialgeschwindigkeit ist die lineare Geschwindigkeit eines Objekts an einem bestimmten Punkt seiner Kreisbahn. Es bezieht sich auf die Größe der Geschwindigkeit eines Objekts in einer Richtung, die an diesem Punkt tangential zur Kurve verläuft.
Winkelbeschleunigung
Die Winkelbeschleunigung, dargestellt durch „α“ (Alpha), ist die Änderung der Winkelgeschwindigkeit pro Zeiteinheit. Wie die Winkelgeschwindigkeit wird sie im Bogenmaß pro Sekunde im Quadrat (rad/s²) gemessen.
Zentripetalbeschleunigung
Die Zentripetalbeschleunigung ist eine Beschleunigung, die auf den Mittelpunkt einer Kreisbahn gerichtet ist. Es tritt auf, wenn sich ein Objekt auf einer gekrümmten Umlaufbahn bewegt und dabei eine ständige Richtungsänderung seiner Geschwindigkeit erfährt, ohne dass sich dies auf seine Größe auswirkt.
Tangentialbeschleunigung
Die Tangentialbeschleunigung ist ein Maß dafür, wie sich die Geschwindigkeit eines sich bewegenden Objekts entlang einer gekrümmten Bahn ändert. Diese Beschleunigung tritt auf, wenn die Tangentialgeschwindigkeit des Objekts variiert.
Berechnungsformeln
Formel für Winkelgeschwindigkeit als Funktion der Zeit
Der Zusammenhang zwischen Anfangswinkelgeschwindigkeit (ω₀), Winkelbeschleunigung (α) und Zeit (t) kann durch die folgende Formel beschrieben werden:
ω= ω₀ + α·t
Wo
- ω ist die Endwinkelgeschwindigkeit.
- ω₀ ist die anfängliche Winkelgeschwindigkeit.
- α ist die Winkelbeschleunigung.
- Es ist Zeit
Formel für gedrehten Winkel
Der Betrag des gedrehten Winkels (θ) zu einem Zeitpunkt „t“ hängt wie folgt von der Winkelgeschwindigkeit und der Winkelbeschleunigung ab:
θ = ω₀·t + ½·α·t²
Wo
- θ ist der gedrehte Winkel.
- ω₀ ist die anfängliche Winkelgeschwindigkeit.
- α ist die Winkelbeschleunigung.
- Es ist Zeit
Formel für Winkelgeschwindigkeit als Funktion der Winkelgeschwindigkeit
Die Endwinkelgeschwindigkeit (ω) hängt mit der Anfangswinkelgeschwindigkeit, der Winkelbeschleunigung und dem Drehwinkel nach der folgenden Formel zusammen:
ω² = ω₀² + 2·α·θ
Wo
- ω ist die Endwinkelgeschwindigkeit.
- θ ist der gedrehte Winkel.
- ω₀ ist die anfängliche Winkelgeschwindigkeit.
- α ist die Winkelbeschleunigung
Anschauliche Alltagsbeispiele
Die gleichmäßig beschleunigte Kreisbewegung (UACM) findet sich in zahlreichen Aspekten des täglichen Lebens und in verschiedenen Kontexten, einige Beispiele sind:
- Wäschewaschmaschine: Beim Schleudern dreht sich die Wäsche in der Trommel mit konstanter Beschleunigung, wodurch das Wasser ausgestoßen wird.
- Fahrgeschäfte auf Fahrgeschäften: Fahrgeschäfte auf Fahrgeschäften wie Riesenräder und Karussells verfügen über eine Start-Stopp-MCUA, um Fahrgästen das Ein- und Aussteigen zu ermöglichen.
- Windkraftanlagen: Windkraftanlagen erleiden einen MCUA, wenn sie in Betrieb gehen oder wenn es Schwankungen in der Windintensität gibt.
- Dampfturbinen: Die Turbinen eines Kernkraftwerks sind darauf optimiert, mit konstanter Drehzahl zu rotieren. Während beim Starten und Stoppen eine gleichmäßig beschleunigte Kreisbewegung auftritt, ist deren Wirkungsgrad geringer.
Gelöste Übungen
Übung 1: Drehung eines Ventilators
Ein Ventilator dreht sich mit einer anfänglichen Winkelgeschwindigkeit von 3 rad/s und erfährt eine Winkelbeschleunigung von 0,5 rad/s². Wie lange wird es dauern, bis eine Winkelgeschwindigkeit von 7 rad/s erreicht ist?
Lösung
Wir verwenden die Formel für die endgültige Winkelgeschwindigkeit:
ω = ω₀ + αt
Wir ersetzen die bekannten Werte:
7 rad/s = 3 rad/s + (0,5 rad/s²) t
Wir lösen für Sie:
(0,5 rad/s²)t = 7rad/s − 3 rad/s
0,5 t = 4 rad/s
t=(4 rad/s) / (0,5 rad/s²) = 8 s
Der Lüfter benötigt 8 s, um eine Winkelgeschwindigkeit von 7 rad/s zu erreichen.
Übung 2: Drehen eines Riesenrads
Ein Riesenrad beginnt sich aus dem Ruhezustand mit einer Winkelbeschleunigung von 0,8 rad/s² zu drehen. Wie lange dauert es, bis sich das Riesenrad um 5 Bogenmaß dreht?
Lösung
Wir verwenden die Formel für den gedrehten Winkel:
θ = ω₀t + ½·α·t²
Wir ersetzen die bekannten Werte:
5rad = (0 rad/s)·t + ½(0,8 rad/s²)·t²
Wir vereinfachen die Gleichung:
5rad = (0,4 rad/s²)t²
Wir lösen für Sie:
t = √( 5 rad / 0,4 rad/s²)
t ≈ 3,54s
Das Riesenrad benötigt etwa 3,54 Sekunden, um sich aus dem Ruhezustand um 5 Bogenmaß zu drehen.
