Die gleichmäßige Kreisbewegung (UCM) ist ein grundlegendes Konzept der Kinematik und beschreibt eine bestimmte Art von Bewegung, bei der sich ein Objekt mit konstanter Geschwindigkeit auf einer Kreisbahn um einen festen Punkt bewegt.
In diesem Artikel definieren wir die MCU und die verschiedenen Grundkonzepte im Zusammenhang mit dieser Bewegung, einige reale Beispiele, die diese Bewegung veranschaulichen, die Formeln für ihre Berechnung und lösen einige Übungen, um sie besser zu verstehen.
Definition der gleichmäßigen Kreisbewegung (MCU)
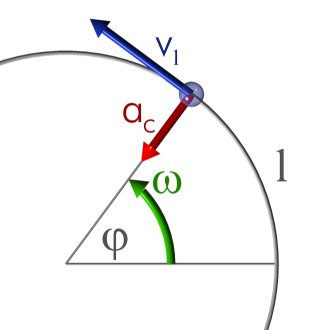Die gleichmäßige Kreisbewegung (UCM) ist eine spezielle Bewegungsart, bei der sich ein Objekt mit konstanter Geschwindigkeit auf einer Kreisbahn um einen festen Punkt bewegt.
In der MCU bleibt die Geschwindigkeit des Objekts auf seinem gesamten Weg in Größe und Richtung unverändert, was bedeutet, dass die Winkelgeschwindigkeit konstant ist.
Eine gleichmäßige Kreisbewegung wird durch das Verhältnis zwischen Winkelgeschwindigkeit und Lineargeschwindigkeit charakterisiert, das in direktem Zusammenhang mit dem Radius der Kreisbahn steht.
Diese Bewegung wird typischerweise in Situationen wie der Umlaufbahn eines Planeten um einen Stern, dem Drehen eines Rades an einem fahrenden Fahrzeug oder sogar in Achterbahn-Vergnügungsparks beobachtet, wo die Passagiere beim Drehen ein konstantes Gefühl von Geschwindigkeit und Richtung verspüren ein zentraler Punkt.
MCU-Grundlagen
Um die MCU zu verstehen, ist es wichtig, sich mit einigen Schlüsselkonzepten vertraut zu machen:
1. Periode (T) und Frequenz (f)
Die Periode (T) ist die Zeit, die das Objekt benötigt, um eine vollständige Umdrehung um die Kreisbahn zu vollenden. Die Frequenz (f) ist die Anzahl der Umdrehungen, die das Objekt in einer Sekunde durchführt. Sie hängen wie folgt zusammen:
f = 1/T
Im Internationalen Einheitensystem (SI) wird die Periode in Sekunden (s) gemessen. Andererseits wird die Frequenz in Hertz (Hz) gemessen. Ein Hertz entspricht einem Zyklus pro Sekunde.
2. Winkelgeschwindigkeit (ω)
Die Winkelgeschwindigkeit (ω) ist ein Maß dafür, wie schnell sich das Objekt auf der Kreisbahn bewegt. Sie wird im Bogenmaß pro Sekunde (rad/s) gemessen und steht in folgendem Verhältnis zur Frequenz (f):
ω = 2·π·f
3. Radius des Pfades (r)
Der Pfadradius (r) ist der Abstand vom Mittelpunkt zum sich bewegenden Objekt in der MCU. Dieser Wert bleibt während der gesamten Bewegung konstant.
4. Lineargeschwindigkeit (v)
Die Lineargeschwindigkeit (v) ist die Geschwindigkeit, mit der sich das Objekt tangential entlang der Kreisbahn bewegt. Aus diesem Grund wird sie auch als Tangentialgeschwindigkeit bezeichnet.
Die Tangentialgeschwindigkeit hängt wie folgt von der Winkelgeschwindigkeit (ω) und dem Radius (r) ab:
v = r·ω
5. Zentripetalbeschleunigung (ac )
Die Zentripetalbeschleunigung (ac ) ist eine fiktive Beschleunigung, die auf das Objekt in einer Richtung entgegen dem Mittelpunkt der Kreisbahn wirkt. Seine Größe hängt wie folgt von der Winkelgeschwindigkeit (ω) und dem Radius (r) ab:
ac =r·ω 2
Die Einheiten der Zentripetalbeschleunigung sind Meter pro Quadratsekunde (m/s²).
Formeln für gleichmäßige Kreisbewegungen
Die folgenden Formeln sind für das Verständnis und die Lösung von Problemen im Zusammenhang mit der MCU unerlässlich:
-
Zusammenhang zwischen Winkelgeschwindigkeit und Lineargeschwindigkeit: v=rω
-
Zusammenhang zwischen Periode und Frequenz: T=1/f
-
Zusammenhang zwischen Winkelgeschwindigkeit und Frequenz: ω=2πf
-
Zusammenhang zwischen Zentripetalbeschleunigung, Winkelgeschwindigkeit und Radius: ac =rω2
Beispiele aus dem Alltag
Gleichmäßige Kreisbewegungen kommen in zahlreichen Bereichen des Alltags vor.
-
Dampfturbinen in Kernkraftwerken: Dampfturbinen in Kernkraftwerken nutzen die MCU, um thermische Energie in mechanische Energie umzuwandeln und so Strom zu erzeugen.
-
Deckenventilatoren: Deckenventilatorflügel sorgen als MCU für eine gleichmäßige Luftzirkulation im Raum und sorgen so für Kühlung.
-
Fahrzeuge in Kurven: Fahrzeuge folgen beim Abbiegen in Kreiskurven einer MCU, die mit diesen Formeln berechnet werden kann.
-
Seilherstellung: Beim Drehen eines Seils zur Herstellung eines Seils wird eine MCU eingesetzt, bei der das Seil gleichmäßig um einen zentralen Kern gewickelt wird.
Gelöste Übungen
Lösen wir nun einige typische Aufgaben rund um die MCU:
Übung 1
Angenommen, ein Rennwagen bewegt sich mit einer konstanten Geschwindigkeit von 100 m/s auf einer Kreisbahn mit einem Radius von 200 Metern. Berechnen Sie die Periode, Frequenz und Winkelgeschwindigkeit der Bewegung.
Lösung:
Da die Geschwindigkeit konstant ist, können wir die Formel für die Winkelgeschwindigkeit verwenden:
v = r·ω
Bekannte Werte ersetzen:
100 m/s = 200 m ⋅ ω
Um ω zu finden:
ω = (100 m/s) / 200 m=0,5 rad/s
Jetzt können wir die Periode (T) mithilfe der Beziehung zwischen Winkelgeschwindigkeit und Frequenz ermitteln:
ω = 2·π·f
0,5 rad/s = 2·π⋅f
Um f zu finden:
f = (0,5 rad/s) / (2·π) ≈ 0,0796 Hz
Und schließlich ist die Periode (T) der Kehrwert der Frequenz:
T = 1/f ≈ 12,57 s
Übung 2
Ein Objekt bewegt sich auf einer Kreisbahn mit einem Radius von 4 Metern und einer Winkelgeschwindigkeit von 2 Bogenmaß pro Sekunde. Berechnen Sie seine Lineargeschwindigkeit und Zentripetalbeschleunigung.
Lösung:
Um die Lineargeschwindigkeit zu ermitteln, verwenden wir die Formel:
v = r·ω
Bekannte Werte ersetzen:
v=4m ⋅ 2 rad/s = 8 m/s
Für die Zentripetalbeschleunigung verwenden wir die Formel:
a c = r·ω 2
Bekannte Werte ersetzen:
a c =4 m⋅(2 rad/s)2=16 m/s 2
